EE 638 – Estimation and Identification (2021)

Review by

Millen Kanabar, 2023 (DD)

Course Offered In

Autumn 2021

Instructors

Debasattam Pal

Prerequisites

Basic math (MA 1xx) courses, probability (EE 325)

Difficulty

Easy-Moderate

Course Content

As the title says, the course has two components- estimation and identification. The identification. Identification was only briefly touched upon; the course's main focus was estimation. The instructor asked for student feedback and structured the course according to the consensus of the class.

Estimation of a deterministic parameter

a. Estimation of a scalar parameter

i.  Cramer-Rao Lower Bound (CRLB) and Fisher information

ii. Estimation of a function of a scalar parameter

b. Estimation of a vector parameter

i.  Extension of the CRLB and Fisher information

ii. Estimation of a function of a vector parameter

c. Minimum variance estimator

i.  Linear models

ii. Sufficient statistics, Rao-Blackwell-Schaffe theorem

d. Best Linear Unbiased Estimator (BLUE)

e. Maximum Likelihood Estimation (MLE)

Estimation of a Stochastic Parameter

a. Bayes’ theorem

b. Minimum Mean Squared Error (MMSE) Estimator

c. Linear Minimum Mean Squared Error (LMMSE) Estimator

d. Weiner filtering

e. Kalman Filter
```
i.  State space representation

ii. Prediction and Innovation
```

Feedback on Lectures The professor was very involved in lectures and took time and effort to ensure that the content got through to students. Doubts were promptly answered, and students were encouraged to discuss and answer throughout class.

Feedback on Evaluations

Evaluation was conducted through quizzes, a midsem, an endsem, and a project. The papers were not lengthy/difficult, and the project was easy to implement. Solving tutorials served as sufficient practice for exam preparation.

Study Material and References

1. Steven M. Kay. Fundamentals of Statistical Signal Processing: Estimation Theory.

Prentice Hall, Upper Saddle River, New Jersey, 1993.

2. Tohru Katayama. Subspace Methods for System Identification. Springer-Verlag, London, 2005.

Follow-up Courses

Final Takeaways

The course was well-structured, and lectures were easy to follow; the instructor cared not to leave anyone behind. The content is sometimes mathematical, and a little abstract, but the tutorials and evaluations help clarify ideas.

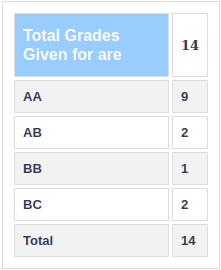
Grading Statistics: Grades